下面是关于考研数学一、二、三中常微分方程部分的考试内容与考试要求对比。

　　数学一常微分方程部分要求：

　　考试内容

　　常微分方程的基本概念、变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、全微分方程、可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程、线性微分方程解的性质及解的结构定理、二阶常系数齐次线性微分方程　高于二阶的某些常系数齐次线性微分方程、简单的二阶常系数非齐次线性微分方程、欧拉(Euler)方程、微分方程的简单应用;

　　考试要求

　　1、了解微分方程及其阶、解、通解、初始条件和特解等概念;

　　2、掌握变量可分离的微分方程及一阶线性微分方程的解法;

　　3、会解齐次微分方程、伯努利方程和全微分方程，会用简单的变量代换解某些微分方程;

　　4、会用降阶法解下列形式的微分方程：

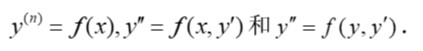
　　5、理解线性微分方程解的性质及解的结构;

　　6、掌握二阶常系数齐次线性微分方程的解法，并会解某些高于二阶的常系数齐次线性微分方程;

　　7、会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程;

　　8、会解欧拉方程;

　　9、会用微分方程解决一些简单的应用问题;

　　数学二常微分方程部分要求：

　　考试内容

　　常微分方程的基本概念、变量可分离的微分方程、齐次微分方程、一阶线性微分方程、可降阶的高阶微分方程、线性微分方程解的性质及解的结构定理、二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程、简单的二阶常系数非齐次线性微分方程　微分方程的简单应用;

　　考试要求

　　1、了解微分方程及其阶、解、通解、初始条件和特解等概念;

　　2、掌握变量可分离的微分方程及一阶线性微分方程的解法，会解齐次微分方程;

　　3、会用降阶法解下列形式的微分方程：

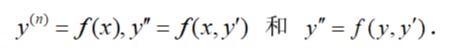
　　4、理解二阶线性微分方程解的性质及解的结构定理;

　　5、掌握二阶常系数齐次线性微分方程的解法，并会解某些高于二阶的常系数齐次线性微分方程;

　　6、会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程;

　　7、会用微分方程解决一些简单的应用问题;

　　数学三常微分方程与差分方程部分要求

　　考试内容

　　常微分方程的基本概念、变量可分离的微分方程、齐次微分方程、一阶线性微分方程、线性微分方程解的性质及解的结构定理、二阶常系数齐次线性微分方程及简单的非齐次线性微分方程、差分与差分方程的概念、差分方程的通解与特解、一阶常系数线性差分方程、微分方程的简单应用;

　　考试要求

　　1、了解微分方程及其阶、解、通解、初始条件和特解等概念。

　　2、掌握变量可分离的微分方程、齐次微分方程和一阶线性微分方程的求解方法。

　　3、会解二阶常系数齐次线性微分方程。

　　4、了解线性微分方程解的性质及解的结构定理，会解自由项为多项式、指数函数、正弦函数、余弦函数的二阶常系数非齐次线性微分方程。

　　5、了解差分与差分方程及其通解与特解等概念。

　　6、了解一阶常系数线性差分方程的求解方法。

　　7、会用微分方程求解简单的经济应用问题。

　　以上就是数一、二、三常微分方程部分的考考试内容与考试要求，希望同学们继续努力!